
Next: Un exemple dans lequel Up: Equation de transport : Previous: Un exemple dans lequel
Des variables auxiliaires
![]() sont introduites aux points
sont introduites aux points
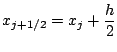 et
et
![]() .
Le schéma de Lax-Wendroff s'écrit :
.
Le schéma de Lax-Wendroff s'écrit :
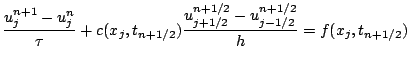
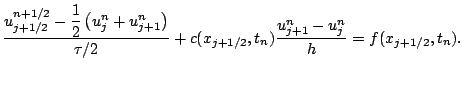
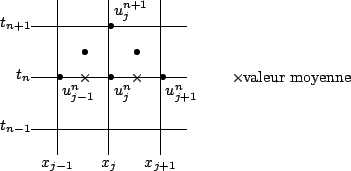
Nous verrons dans la suite que ce schéma est stable si
![]() .
.