Programmation à l'aide du logiciel Matlab

Le logiciel Matlab est un outil très performant pour la résolution de grands systèmes linéaires. L'utilisation de Matlab permet de faire des expériences numériques sans avoir à programmer en C ou Fortran.

Matlab contient une bibliothèque numérique très complète pour la résolution de grands systèmes linéaires creux (tapez help sparfun pour avoir des précisions). Par exemple, vous pouvez effectuer la décomposition de Choleski d'une matrice bande en procédant de la manière suivante.

M=5
I = speye(M,M);
E = sparse(2:M,1:M-1,1,M,M);
D = -E-E'+2*I;
A = kron(D,I)+kron(I,D);
spy(A);
[R,p]=chol(A);
spy(R);
N=M*M
b = zeros([N,1]);
for i=1:M
  b(i) = b(i)+i;
end
for i=1:M
  b(M*(i-1)+1) = b(M*(i-1)+1)+i;
end
for i=1:M
  b(M*(i-1)+M) = b(M*(i-1)+M)+M+1+i;
end
for i=1:M
  b(M*(M-1)+i) = b(M*(M-1)+i)+M+1+i;
end
x=R\(R'\b)

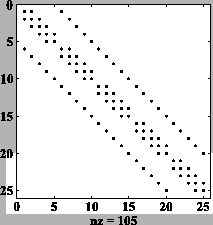
Voici les coefficients non nuls de la matrice $A$ (spy(A) dans le script Matlab) :

Voici les coefficients non nuls de la matrice $L$ (spy(R') dans le script Matlab) :

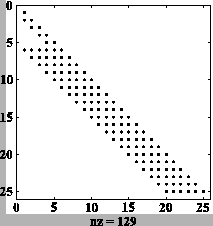
Nous observons bien que les matrices $A$ et $L$ ont même largeur de bande. Néanmoins, nous constatons que la matrice $L$ est moins creuse que la matrice $A$.

Voici le résultat du calcul Matlab :

x =

    2.0000
    3.0000
    4.0000
    5.0000
    6.0000
    3.0000
    4.0000
    5.0000
    6.0000
    7.0000
    4.0000
    5.0000
    6.0000
    7.0000
    8.0000
    5.0000
    6.0000
    7.0000
    8.0000
    9.0000
    6.0000
    7.0000
    8.0000
    9.0000
   10.0000