Dérivées numériques d'ordre un

Soit $f:\mathbb{R}\to\mathbb{R}$ une fonction continue, de première dérivée continue et soit $x_0\in\mathbb{R}$. Il s'agit d'approcher numériquement $f'(x_0)$. Pour ce faire, on choisit $h>0$ ``petit'' et on utilise les formules de différences finies progressive, rétrograde et centrée, respectivement définies par

$$\dfrac{\Delta_{h} f(x_{0})}{h}=\dfrac{f(x_0+h)-f(x_0)}{h}$$

$$\dfrac{\nabla_{h} f(x_{0})}{h}=\dfrac{f(x_0)-f(x_0-h)}{h}$$

$$\dfrac{\delta_{h} f(x_{0})}{h} =\dfrac{f(x_0+h/2)-f(x_0-h/2)}{h}$$

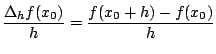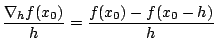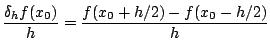Erreur de troncature

D'après la section 2.1 du livre, l'erreur de troncature est d'ordre 1 pour les formules de différences finies progressive et rétrograde et d'ordre 2 pour la formule de différences finies centrée. Nous noterons :

$$\left\vert f'(x_{0}) - \dfrac{\Delta_{h} f(x_{0})}{h} \right\vert =O(h),$$

$$\left\vert f'(x_{0}) - \dfrac{\nabla_{h} f(x_{0})}{h} \right\vert =O(h),$$

$$\left\vert f'(x_{0}) - \dfrac{\delta_{h} f(x_{0})}{h} \right\vert =O(h^2),$$

pour plus de précisions, voir les théorèmes 2.2 et 2.3 du livre.

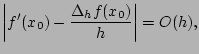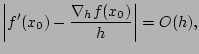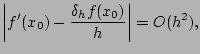Erreur d'arrondis

Sur un ordinateur, les nombres sont mémorisés avec un nombre fini de chiffres significatifs (8 pour les ``float'', 16 pour les ``double''). A l'erreur de troncature s'ajoute donc l'erreur d'arrondis qui, pour le calcul des dérivées premières, est en $O(1/h)$ (voir la section 2.2 du livre). L'erreur totale est donc la somme de ces deux erreurs.

Illustration des erreurs de troncature et d'arrondis

Soit $f$ la fonction définie par $f(x) = x^{5}-5x^{3}+4x$, on pose $x_0=0.6$, il s'agit d'approcher $f'(x_0)$ à l'aide des formules de différences finies progressive, rétrograde et centrée. L'applet suivante effectue ces calculs pour des valeurs de $h$ de plus en plus petites et permet de vérifier les ordres de convergence annoncés.

Nous interprétons les résultats de la manière suivante: lorsque $h$ est "raisonnablement petit", l'effet dû aux erreurs de troncature est prépondérant, la pente des courbes ainsi obtenues indique l'ordre de convergence de chacune des formules de différences finies. Conformément aux prédictions théoriques, nous observons que

• les formules de différences finies progressive et rétrograde convergent à l'ordre $1$ en $h$,
• la formule de différences finies centrée converge à l'ordre $2$ en $h$.

Lorsque $h$ est "trop petit", l'effet dû aux erreurs d'arrondis devient prépondérant. Conformément aux prédictions théoriques nous observons que l'erreur croît en $1/h$.