Position du problème

Dans ce chapitre, nous considérons un problème de convection-diffusion évolutif (voir aussi les exercices 14.1 et 14.2 du livre). Soit 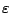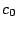$\varepsilon$, $c_0$ deux nombres réels positifs. Soit

$$w:x\in[0,1] \to w(x)\in\mathbb{R},$$

$$f:(x,t)\in[0,1]\times\mathbb{R}^+ \to f(x,t)\in\mathbb{R},$$

deux fonctions données. Dans ce chapitre, nous cherchons une fonction

$$u:(x,t)\in[0,1]\times\mathbb{R}^+ \to u(x,t)\in\mathbb{R},$$

telle que

$$\dfrac{\partial u}{\partial t}(x,t) -\varepsilon\dfrac{\partial^2... ...{\partial u}{\partial x}(x,t)=f(x,t) \qquad \forall x\in]0,1[,\quad\forall t>0,$$ (14.1)

$$u(x,0)=w(x) \qquad \forall x\in]0,1[,$$ (14.2)

$$u(0,t)=u(1,t)=0 \qquad \forall t>0.$$ (14.3)

L'équation (14.1) est une équation de convection-diffusion évolutive. Le deuxième terme de cette équation modélise le phénomène de diffusion et le troisième terme, le phénomène de convection. L'équation (14.2) est la condition initiale, les équations (14.3) sont les conditions aux limites.