
Next: Cas particulier : équation Up: Position du problème Previous: Position du problème
Si
![]() , l'équation (14.1)
se réduit à une équation de transport (voir le chapitre 13
du livre).
Dans ce cas la condition aux limites
, l'équation (14.1)
se réduit à une équation de transport (voir le chapitre 13
du livre).
Dans ce cas la condition aux limites
![]() doit être supprimée.
doit être supprimée.
Supposons encore que ![]() ,
il est facile de vérifier que la fonction
,
il est facile de vérifier que la fonction ![]() définie par
définie par
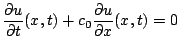 |
||||
EPFL-IACS-ASN