
Next: Chap. 4 : Elimination Up: Chap. 3 : Intégration Previous: Exercice : vérification des
Voici, en fonction de ![]() , l'erreur entre
, l'erreur entre
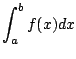 et
et
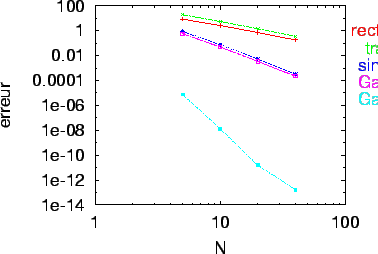
Nous vérifions que les formules du rectangle et du trapèze convergent
à l'ordre 2 (pente 2 en échelle log-log).
Les formules de Simpson et de Gauss à deux points convergent
à l'ordre 4,
la formule de Gauss à 5 points à l'ordre
10 (l'erreur est donc divisée par
![]() chaque fois que
chaque fois que ![]() est divisé par
est divisé par ![]() ).
).