
Next: L'algorithme Up: L'algorithme d'élimination de Gauss Previous: L'algorithme d'élimination de Gauss
Première étape
Divisons la première
ligne par ![]() et additionnons la nouvelle première ligne à la deuxième :
et additionnons la nouvelle première ligne à la deuxième :
 |
Deuxième étape
Divisons la deuxième ligne par ![]() et
additionnons la nouvelle deuxième ligne à la troisième :
et
additionnons la nouvelle deuxième ligne à la troisième :
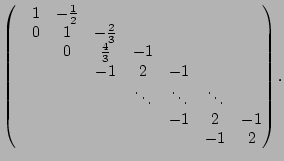 |
 |
Il est important de ne pas inverser la matrice ![]() lors de la
résolution de
lors de la
résolution de
![]() . En effet, à l'aide du logiciel
Matlab (voir par exemple la fin de ce chapitre),
nous pouvons inverser la matrice
. En effet, à l'aide du logiciel
Matlab (voir par exemple la fin de ce chapitre),
nous pouvons inverser la matrice ![]() et constater que
et constater que ![]() est une matrice pleine. De telles opérations
sont très coûteuses en temps et en mémoire.
est une matrice pleine. De telles opérations
sont très coûteuses en temps et en mémoire.
EPFL-IACS-ASN