Soit 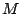 un entier positif, et soit
un entier positif, et soit 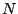 tel que
tel que 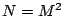 . Dans la
section 11.3 du livre, nous avons à résoudre un système linéaire
. Dans la
section 11.3 du livre, nous avons à résoudre un système linéaire
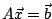 , la matrice
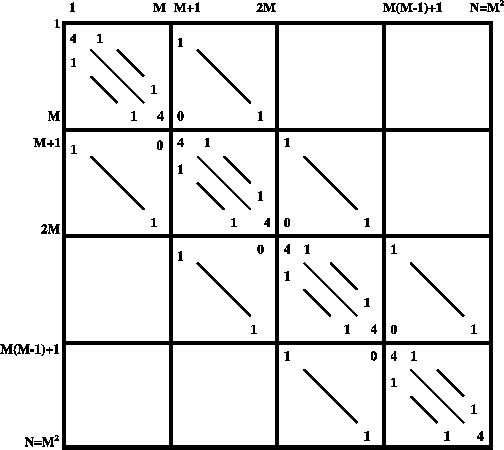
, la matrice 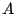 étant définie par la figure ci-dessous.
étant définie par la figure ci-dessous.
Cette matrice est clairement symétrique et de bande de demi-largeur 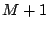 .
D'après le théorème 11.1, elle est définie positive et nous pouvons
effectuer sa décomposition de Cholesky
.
D'après le théorème 11.1, elle est définie positive et nous pouvons
effectuer sa décomposition de Cholesky 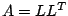 puis effectuer les deux
résolutions
puis effectuer les deux
résolutions
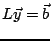 et
et
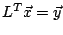 pour résoudre
le système linéaire. Dans la suite
nous proposons un programme effectuant ces opérations, soit
en utilisant la bibliothèque numérique
Lapack,
soit le logiciel
Matlab.
pour résoudre
le système linéaire. Dans la suite
nous proposons un programme effectuant ces opérations, soit
en utilisant la bibliothèque numérique
Lapack,
soit le logiciel
Matlab.
Considérons le cas où le 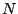 -vecteur
-vecteur 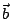 a pour coefficients
a pour coefficients
les autres coefficients étant nuls. Nous pouvons alors vérifier que
le 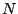 -vecteur
-vecteur 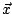 a pour coefficients
a pour coefficients
Nous utiliserons ce résultat pour valider nos programmes.
EPFL-IACS-ASN

![]() un entier positif, et soit
un entier positif, et soit ![]() tel que
tel que ![]() . Dans la
section 11.3 du livre, nous avons à résoudre un système linéaire
. Dans la
section 11.3 du livre, nous avons à résoudre un système linéaire
![]() , la matrice
, la matrice ![]() étant définie par la figure ci-dessous.
étant définie par la figure ci-dessous.
![]() -vecteur
-vecteur ![]() a pour coefficients
a pour coefficients