Considérons à nouveau le système linéaire du chapitre 5 du support de
cours.
Soit 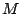 un entier positif, et soit
un entier positif, et soit 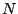 tel que
tel que 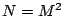 . Dans la
section 11.3 du livre nous avons à résoudre un système linéaire
. Dans la
section 11.3 du livre nous avons à résoudre un système linéaire
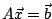 , la matrice
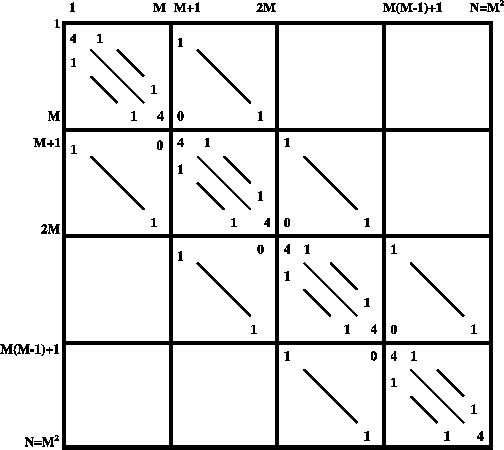
, la matrice 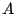 étant définie par la figure ci-dessous.
étant définie par la figure ci-dessous.
Cette matrice est clairement symétrique, de bande de demi-largeur 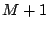 .
D'après le théorème 11.1, elle est définie positive et nous pouvons
utiliser l'algorithme du gradient conjugué pour résoudre
le système linéaire. D'après le théorème 6.7, l'algorithme
converge en au plus
.
D'après le théorème 11.1, elle est définie positive et nous pouvons
utiliser l'algorithme du gradient conjugué pour résoudre
le système linéaire. D'après le théorème 6.7, l'algorithme
converge en au plus 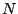 itérations. En pratique, nous constaterons
qu'il faut de l'ordre de
itérations. En pratique, nous constaterons
qu'il faut de l'ordre de 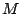 itérations, soit
beaucoup moins que le résultat annoncé dans le théorème 6.7.
itérations, soit
beaucoup moins que le résultat annoncé dans le théorème 6.7.
Considérons le cas où le 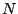 -vecteur
-vecteur 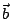 a pour coefficients
a pour coefficients
les autres coefficients étant nuls. Nous pouvons alors vérifier que
le 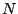 -vecteur
-vecteur 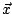 a pour coefficients
a pour coefficients
Nous utiliserons ce résultat pour valider les calculs.
EPFL-IACS-ASN

![]() un entier positif, et soit
un entier positif, et soit ![]() tel que
tel que ![]() . Dans la
section 11.3 du livre nous avons à résoudre un système linéaire
. Dans la
section 11.3 du livre nous avons à résoudre un système linéaire
![]() , la matrice
, la matrice ![]() étant définie par la figure ci-dessous.
étant définie par la figure ci-dessous.
![]() -vecteur
-vecteur ![]() a pour coefficients
a pour coefficients