Programmation à l'aide du logiciel Matlab

Le logiciel Matlab est un outil très performant pour la résolution de grands systèmes linéaires. L'utilisation de Matlab permet de faire des expériences numériques sans avoir à programmer en C ou Fortran.

Matlab contient une bibliothèque numérique très complète pour la résolution de grands systèmes linéaires creux (tapez help sparfun pour avoir des précisions). Par exemple, vous pouvez résoudre le système linéaire en question en utilisant la fonction pcg.

M=5
I = speye(M,M);
E = sparse(2:M,1:M-1,1,M,M);
D = -E-E'+2*I;
A = kron(D,I)+kron(I,D);
spy(A);
N=M*M;
b = zeros([N,1]);
for i=1:M
  b(i) = b(i)+i;
end
for i=1:M
  b(M*(i-1)+1) = b(M*(i-1)+1)+i;
end
for i=1:M
  b(M*(i-1)+M) = b(M*(i-1)+M)+M+1+i;
end
for i=1:M
  b(M*(M-1)+i) = b(M*(M-1)+i)+M+1+i;
end
x=pcg(A,b,1.e-6,500);

Voici les coefficients non nuls de la matrice $A$ (spy(A) dans le script Matlab) :

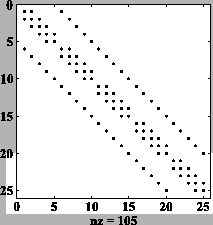
voici le résultat pour $M=5$ :

pcg converged at iteration 11 to a solution with relative residual 6e-16

Le nombre d'itérations en fonction de $M$ est reporté dans le tableau suivant :

$M$	itérations
5	11
10	25
20	49
40	96
80	187
160	360

Nous observons donc que

• Le nombre d'itérations augmente lorsque $M$ augmente.
• Le nombre d'itérations est environ multiplié par deux lorsque $M$ est multiplié par deux.