Préconditionnement

Du point de vue théorique, on peut montrer que le nombre d'itérations nécessaire à la résolution de $A\vec{x}=\vec{b}$ avec l'algorithme du gradient conjugué dépend du nombre de condition spectral de $A$ :

$$\chi (A) = \frac{\max\limits_{1 \leq j \leq N} \mid \lambda_{j} \mid} {\min\limits_{1 \leq j \leq N} \mid \lambda_{j} \mid},$$

les réels $\lambda_j$, $1\le j\le N$ étant les valeurs propres de $A$. Ainsi, en pratique, au lieu de résoudre $A\vec{x}=\vec{b}$ avec l'algorithme du gradient conjugué, il convient de résoudre $C^{-1}A\vec{x}=C^{-1}\vec{b}$, où $C$ est une matrice symétrique définie positive choisie de sorte que

• $\chi(C^{-1}A)$ soit nettement plus petit que $\chi(A)$,
• la résolution d'un système linéaire du type $C\vec{y}=\vec{c}$ doit être nettement moins coûteuse que la résolution de $A\vec{x}=\vec{b}$.

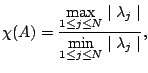
Un certain nombre de préconditionneurs sont à disposition dans Matlab. Par exemple, vous pouvez utiliser la décomposition de Cholesky incomplète :

M=5
I = speye(M,M);
E = sparse(2:M,1:M-1,1,M,M);
D = -E-E'+2*I;
A = kron(D,I)+kron(I,D);
spy(A);
N=M*M;
b = zeros([N,1]);
for i=1:M
  b(i) = b(i)+i;
end
for i=1:M
  b(M*(i-1)+1) = b(M*(i-1)+1)+i;
end
for i=1:M
  b(M*(i-1)+M) = b(M*(i-1)+M)+M+1+i;
end
for i=1:M
  b(M*(M-1)+i) = b(M*(M-1)+i)+M+1+i;
end
Rinc=cholinc(A,'0');
spy(Rinc');
x=pcg(A,b,1.e-6,500,Rinc',Rinc);

Voici les coefficients non nuls de la décomposition de Cholesky incomplète (spy(Rinc') dans le script Matlab) :

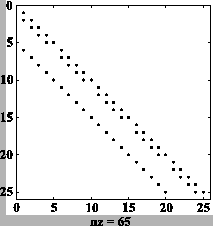
Par conséquent, l'algorithme du gradient conjugué préconditionné par la décomposition de Cholesky incomplète nécessite deux fois plus de mémoire que l'algorithme du gradient conjugué (sans préconditionneur).

Voici le résultat du script Matlab pour $M=5$ :

pcg converged at iteration 7 to a solution with relative residual 3.9e-07

A l'aide des fonctions flops et whos de Matlab, nous avons comparé le nombre d'itérations ainsi que le nombre d'opérations nécessaire à la mise en oeuvre de l'algorithme du gradient conjugué (sans préconditionneur) et l'algorithme du gradient conjugué préconditionné par la décomposition de Cholesky incomplète, ceci pour différentes valeurs de $M$.

Le nombre d'itérations en fonction de $M$ est reporté dans le tableau suivant :

$M$	sans préconditionneur	avec préconditionneur
20	49	18
40	96	32
80	187	60
160	360	108

Le nombre d'opérations (en millions) est reporté dans le tableau suivant :

$M$	sans préconditionneur	avec préconditionneur
20	0.694	0.359
40	5.48	2.56
80	42.8	19.2
160	331	138

Nous concluons donc en affirmant que l'algorithme du gradient conjugué préconditionné par la décomposition de Cholesky incomplète est plus rapide que l'algorithme du gradient conjugué non préconditionné, mais nécessite deux fois plus de mémoire.