Méthode directe ou méthode itérative ?

Il s'agit maintenant d'estimer la mémoire et le nombre d'opérations nécessaires à la résolution du système linéaire $A\vec{x}=\vec{b}$. Nous considérons les cas suivants :

• Méthode directe : le système linéaire est résolu en utilisant la décomposition de Cholesky.
• Méthode itérative : le système linéaire est résolu en utilisant l'algorithme du gradient conjugué.

La décomposition de Cholesky de la matrice $A$ nécessite le stockage de la bande, soit $N\times M=M^3$ coefficients. Le nombre d'opérations nécessaire à la décomposition est d'ordre $N\times M^2=M^4$ (théorème 5.4 du livre).

En ce qui concerne l'algorithme du gradient conjugué, seuls les éléments non-nuls de la matrice $A$ doivent être stockés, soit moins de $5N=5M^2$ coefficients. Les expériences numériques montrent que le nombre d'itérations nécessaire à la convergence de l'algorithme est d'ordre $M$. A chaque itération, le coût principal est celui d'une multiplication matrice-vecteur, soit moins de $5N=5M^2$ opérations. Par conséquent, le nombre d'opérations de l'algorithme du gradient conjugué est de l'ordre de $M^3$.

Les résultats sont résumés dans le tableau ci-dessous.

méthode	mémoire	opérations
directe	$O(M^3)$	$O(M^4)$
itérative	$O(M^2)$	$O(M^3)$

A l'aide des fonctions flops et whos de Matlab, nous avons comparé le nombre d'opérations ainsi que la mémoire nécessaire à la mise en oeuvre des deux algorithmes pour différentes valeurs de $M$ (pour la mise en oeuvre de la décomposition de Cholesky avec Matlab, voir le chapitre 5 du support de cours).

Le nombre d'opérations (en millions) est reporté dans le tableau suivant :

$M$	méthode directe	méthode itérative
20	0.197	0.694
40	2.86	5.48
80	43.3	42.8
160	674	331

Nous observons donc que

• Méthode directe : le nombre d'opérations est environ multiplié par $2^4=16$ chaque fois que $M$ est multiplié par deux : le nombre d'opérations est bien d'ordre $M^4$.
• Méthode itérative : le nombre d'opérations est environ multiplié par $2^3=8$ chaque fois que $M$ est multiplié par deux : le nombre d'opérations est bien d'ordre $M^3$.
• Pour $M\ge 80$, la méthode itérative nécessite moins d'opérations que la méthode directe.

En ce qui concerne la place mémoire, rappelons que pour $M=5$ les coefficients non-nuls des matrices $A$ et $L$ (avec $A=LL^T$) sont

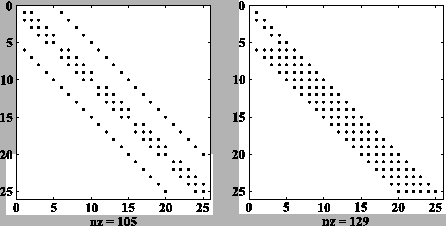
La place mémoire nécessaire au stockage de $A$ et $L$ (en millions de ``double'') est reporté dans le tableau suivant :

$M$	mémoire pour $A$	mémoire pour $L$
20	0.0294	0.0978
40	0.119	0.775
80	0.482	6.17
160	1.94	49.2

Nous observons donc que

• Méthode directe : la place mémoire nécessaire au stockage de $A$ est environ multiplié par $2^3=8$ chaque fois que $M$ est multiplié par deux : la place mémoire nécessaire au stockage de $A$ est bien d'ordre $M^3$.
• Méthode itérative : la place mémoire nécessaire au stockage de $L$ est environ multiplié par $2^2=4$ chaque fois que $M$ est multiplié par deux : la place mémoire nécessaire au stockage de $L$ est bien d'ordre $M^2$.
• La méthode itérative nécessite toujours moins de place mémoire que la méthode directe.

Nous concluons donc en affirmant que, lorsque $M$ est grand, l'algorithme du gradient conjugué est plus performant que la décomposition de Cholesky pour la résolution du système linéaire $A\vec{x}=\vec{b}$, la matrice $A$ étant définie par la figure ci-dessous.

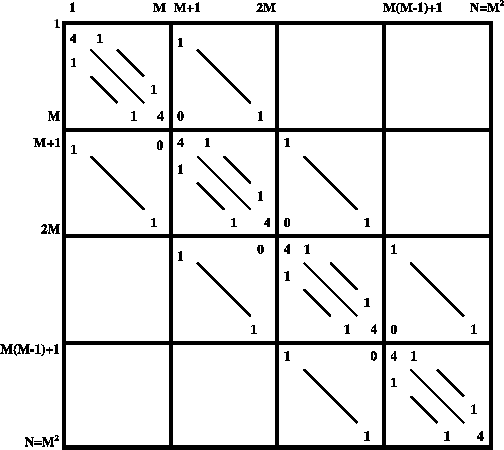
Ces résultats sont généralisables au cas où la matrice $A$ est celle obtenue lorsqu'on utilise une méthode d'éléments finis continus de degré un (voir la section 11.2 du livre).