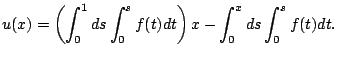Next: Méthode des différences finies Up: Chap. 10 : Différences Previous: Chap. 10 : Différences
Considérons le problème du déplacement
vertical ![]() au point
au point ![]() d'une corde tendue
entre les extrémités
d'une corde tendue
entre les extrémités ![]() et
et ![]() ,
soumise à une tension unité et à une densité de charge
verticale
,
soumise à une tension unité et à une densité de charge
verticale ![]() . Le problème correspondant s'énonce :
trouver une fonction
. Le problème correspondant s'énonce :
trouver une fonction ![]() deux fois continûment dérivable
sur
deux fois continûment dérivable
sur
![]() telle que
telle que
![]() L'équation (10.1) est une équation différentielle linéaire du second ordre.
L'équation (10.1) est une équation différentielle linéaire du second ordre.
![]() Les égalités (10.2) sont appelées ``conditions aux limites''.
Les égalités (10.2) sont appelées ``conditions aux limites''.
![]() Le problème (10.1),(10.2) est appelé ``problème du second ordre aux limites 1D''.
Le problème (10.1),(10.2) est appelé ``problème du second ordre aux limites 1D''.
![]() En intégrant (10.1) une fois, on obtient :
En intégrant (10.1) une fois, on obtient :