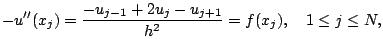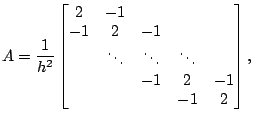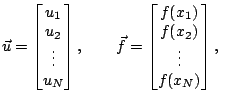Soit 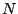 un entier positif, on pose
un entier positif, on pose
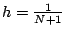 ,
, 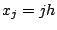 ,
,
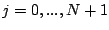 .
.

Pour tout
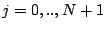 , on approche
, on approche 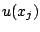 par la valeur
par la valeur 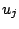 définie par :
définie par :
Nous obtenons ainsi le système linéaire
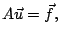 |
(10.4) |
où 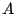 est la
est la
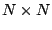 matrice définie par
matrice définie par
et les 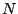 -vecteurs
-vecteurs 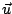 et
et 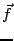 sont donnés par
sont donnés par
La matrice 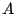 étant tridiagonale symétrique définie positive,
on résout le système (10.4) par la méthode de Cholesky
(voir le chapitre 5 du livre).
étant tridiagonale symétrique définie positive,
on résout le système (10.4) par la méthode de Cholesky
(voir le chapitre 5 du livre).
Si 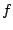 est 4 fois continûment dérivable, on a l'estimation d'erreur
suivante :
où
est 4 fois continûment dérivable, on a l'estimation d'erreur
suivante :
où 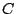 ne dépend pas de
ne dépend pas de 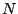 (et donc pas de
(et donc pas de 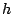 ).
).
Avec l'exemple interactif ci-dessous, vous pouvez visualiser
l'approximation de 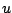 par différences finies.
par différences finies.
EPFL-IACS-ASN

![]() un entier positif, on pose
un entier positif, on pose
![]() ,
, ![]() ,
,
![]() .
.
![]()
![]() , on approche
, on approche ![]() par la valeur
par la valeur ![]() définie par :
définie par :