Exemples numériques

Dans cette section, nous appliquons la méthode numérique que nous venons de décrire. Pour cela, nous avons utilisé le logiciel Matlab (pour plus de détails voir la section suivante : utilisation du logiciel Matlab).

On considère à nouveau $\Omega_{\alpha}$ comme étant le disque unité privé d'un secteur circulaire d'ouverture $\alpha$, et on prend $f(x)=1, \ \forall x \in \Omega$. Pour différentes ouvertures ( $\alpha = 0, \alpha = 30, \alpha = 60, \alpha = 90, \alpha = 180, \alpha = 270$ degrés) nous avons construit des triangulations $\Omega_{\alpha,h}$ des domaines $\Omega_{\alpha}$. La taille moyenne des triangles étant à peu près la même dans chacun des cas, les triangulations contiennent de $1079$ noeuds et $2080$ triangles (pour $\Omega_{270,h}$) à $2281$ noeuds et $4384$ triangles ( pour $\Omega_{0,h}$). Nous avons ensuite calculé la solution $u_h$ relative aux différents domaines considérés.
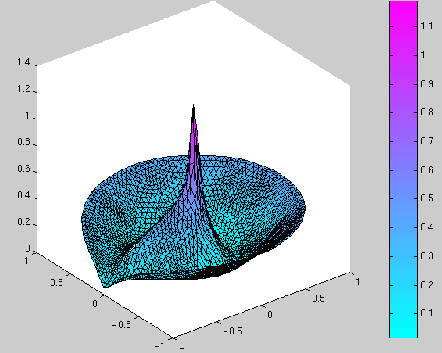
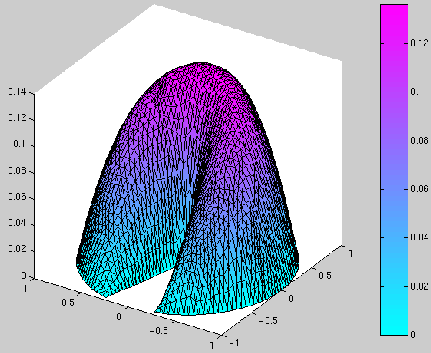
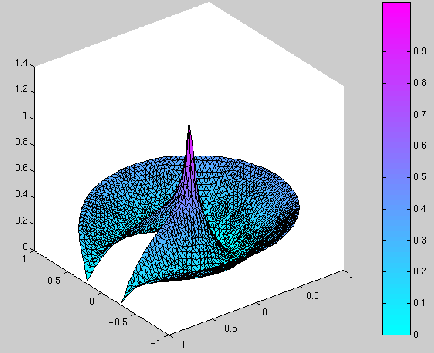
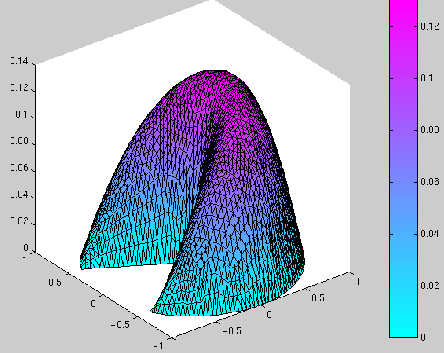
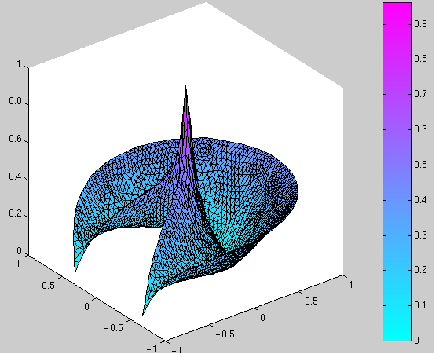
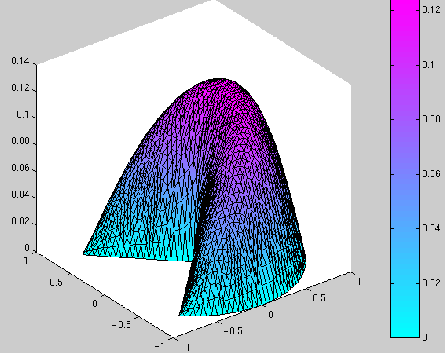
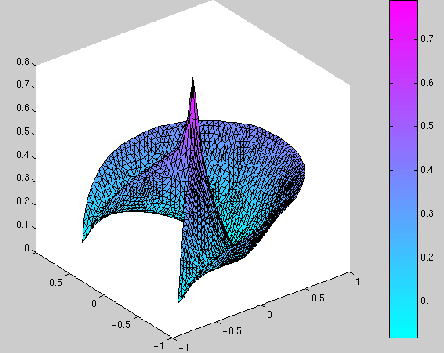
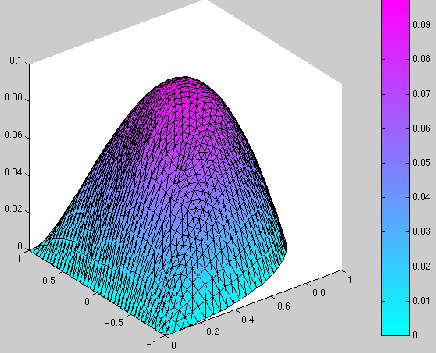
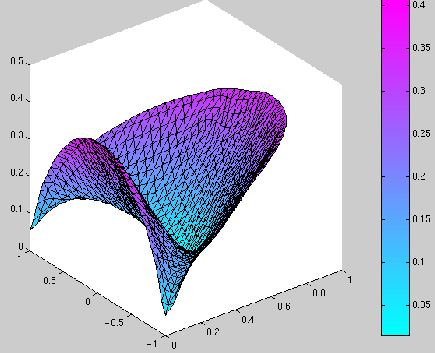
Ci-dessous, nous avons représenté les résultats de la manière suivante : pour $\alpha$ donné ( $\alpha = 0,30,60,90,180,270$), nous avons construit deux graphiques en 3D. Dans un premier graphique : $\left\{ (x_1,x_2,u_h(x_1,x_2)) , (x_1,x_2) \in \Omega_{\alpha} \right\}$, on a représenté la fonction $u_h$ sur le domaine $\Omega_{\alpha}$, et dans le deuxième : $\left\{ (x_1,x_2,\Vert \overrightarrow{\mbox{grad}} u_h(x_1,x_2) \Vert) , (x_1,x_2) \in \Omega_{\alpha} \right\}$ la norme de $\overrightarrow{\mbox{grad}} u_h$.

$\alpha=0$

$\alpha=30$

$\alpha=60$

$\alpha=90$

$\alpha=180$

$\alpha=270$

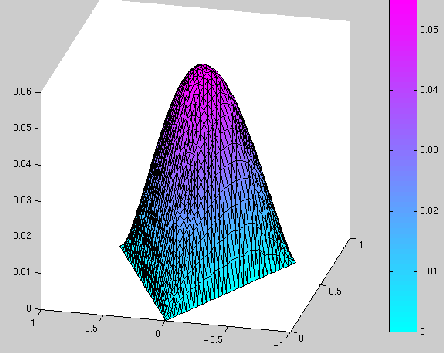
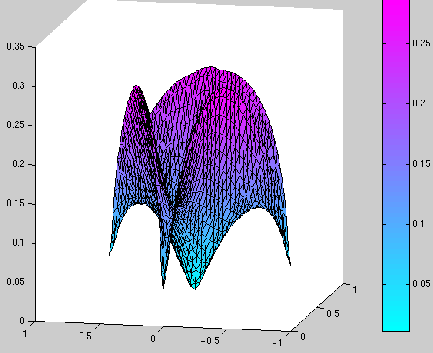
Nous remarquons donc que, si $\alpha$ est supérieur à 180 degrés, alors la solution du problème est régulière au sens où $\overrightarrow{\mbox{grad}} u$ ne présente pas de pic au point $(0,0)$. On peut montrer que cette propriété est liée au fait que le domaine de calcul $\Omega_\alpha$ est convexe lorsque $\alpha$ est supérieur à 180 degrés.