
Next: Exemples numériques Up: Chap. 11 : Une Previous: Mise sous forme matricielle
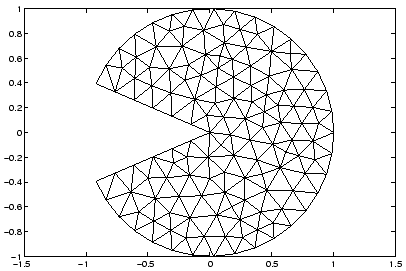
2) A chaque noeud intérieur
![]() on associe une fonction
on associe une fonction
![]() de
de
![]() dans
dans
![]() . La fonction
. La fonction
![]() , est définie par
, est définie par
![]() est nulle en tous les noeuds de
est nulle en tous les noeuds de
![]() sauf au point
sauf au point
![]() où elle vaut 1,
où elle vaut 1,
![]() est un polynôme de degré un sur chaque triangle
est un polynôme de degré un sur chaque triangle
![]() .
.
( Dans la figure 11.3 du livre, on trouvera une représentation graphique d'une
telle fonction ![]() . )
. )
3) On construit la matrice dite de rigidité ![]() et
le second membre
et
le second membre ![]() donnés par (11.5).
donnés par (11.5).
4) On résout le système linéaire (11.6).
La matrice ![]() est creuse au sens où la plupart de ses coefficients sont
nuls. En effet, nous avons
est creuse au sens où la plupart de ses coefficients sont
nuls. En effet, nous avons ![]() si
si ![]() et
et ![]() ne
sont pas des sommets voisins (i.e. ayant une arête commune).
Voici l'allure de
ne
sont pas des sommets voisins (i.e. ayant une arête commune).
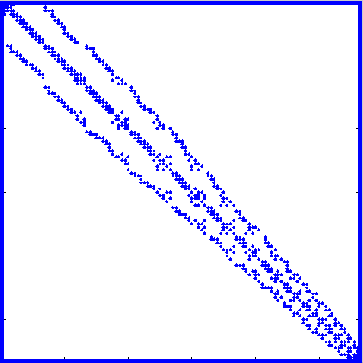
Voici l'allure de ![]() dans le cas présent
(les coefficients non-nuls sont représentés par un carré bleu).
dans le cas présent
(les coefficients non-nuls sont représentés par un carré bleu).
Du point de vue infomatique,
il est hors de question de stocker tous les coefficients de la matrice ![]() .
La méthode de stockage dépend de la méthode de résolution du système
linéaire. Si le système linéaire est résolu à l'aide d'une méthode
directe (décomposition LU de Cholesky ou élimination de Gauss, voir les chap. 4 et 5 du livre), alors on utilise
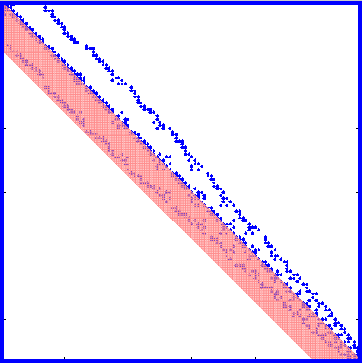
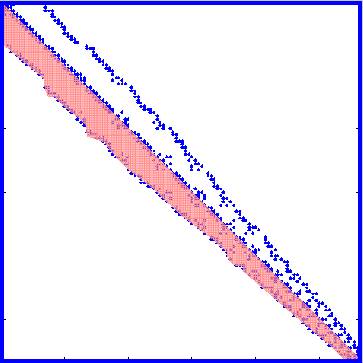
alors le stockage bande (fig. de gauche) ou profil (fig. de droite).
.
La méthode de stockage dépend de la méthode de résolution du système
linéaire. Si le système linéaire est résolu à l'aide d'une méthode
directe (décomposition LU de Cholesky ou élimination de Gauss, voir les chap. 4 et 5 du livre), alors on utilise
alors le stockage bande (fig. de gauche) ou profil (fig. de droite).
Si le système linéaire est résolu à l'aide d'une méthode itérative (gradient conjugué, GMRES, voir le chap. 6 du livre), alors on ne stocke que les coefficients non nuls de la matrice.
EPFL-IACS-ASN