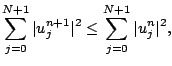En reprenant les mêmes arguments que ceux utilisés pour les schémas d'Euler,
on montre sans difficulté que si
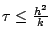 , alors on a
, alors on a
pour autant que 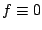 . Si
. Si
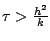 on perd malheureusement
cette stabilité dite en norme du maximum. En revanche, on peut montrer que,
quel que soit le pas de temps
on perd malheureusement
cette stabilité dite en norme du maximum. En revanche, on peut montrer que,
quel que soit le pas de temps 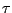 choisi, on a toujours (lorsque
choisi, on a toujours (lorsque 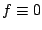 )
)
et on parle de stabilité en norme quadratique. Le schéma de Crank-Nicholson
est inconditionnellement stable en norme quadratique.
Comme vous pouvez le constater sur l'exemple interactif suivant,
il n'y a pas de limitation sur le pas de temps
semblable à (12.23). En revanche, des oscillations peuvent se produire
lorsque
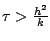 .
.
EPFL-IACS-ASN

![]() , alors on a
, alors on a