Considérons les schémas (12.20)-(12.22) et
supposons que le pas de temps est choisi de sorte que la condition de stabilité
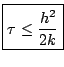 |
(12.23) |
est satisfaite.
Nous avons ainsi
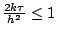 . Si nous admettons maintenant que
. Si nous admettons maintenant que 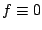 (source de chaleur nulle) alors (12.20) devient :
et par suite, en constatant que
(source de chaleur nulle) alors (12.20) devient :
et par suite, en constatant que 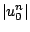 et
et 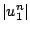 sont majorés
par
sont majorés
par
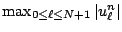 :
:
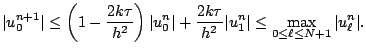 |
(12.24) |
De même (12.21) devient :
et par suite :
De la même manière nous obtenons à partir de (12.22) que
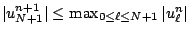 .
.
Nous avons donc prouvé que, sous la condition de stabilité
(12.23), nous avons
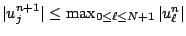 pour tout
pour tout
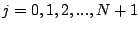 et donc
et donc
L'exemple interactif suivant illustre la
décroissance du maximum de la température sous la condition de
stabilité (12.23). Si nous avons le malheur de prendre
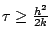 ,
alors ce résultat n'est plus vrai et nous assistons au développement
d'instabilités numériques. Dans ce cas nous dirons que le schéma
est instable dans la norme du maximum.
,
alors ce résultat n'est plus vrai et nous assistons au développement
d'instabilités numériques. Dans ce cas nous dirons que le schéma
est instable dans la norme du maximum.
EPFL-IACS-ASN

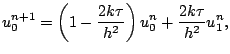
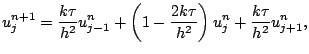
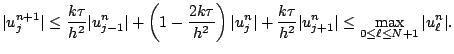
![]() pour tout
pour tout
![]() et donc
et donc