Supposons que
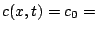 constante et
constante et
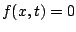 . Le problème
(13.1) et (13.2) devient alors
. Le problème
(13.1) et (13.2) devient alors
| |
|
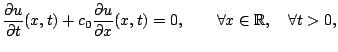 |
(13.3) |
| |
|
|
|
| |
|
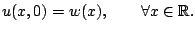 |
(13.4) |
La solution de ce problème est donnée par :
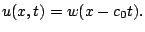 |
(13.5) |
Ainsi, la condition initiale 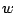 est transportée le long de l'axe
est transportée le long de l'axe 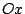 avec
la vitesse
avec
la vitesse 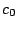 . Vous pouvez visualiser
la solution
. Vous pouvez visualiser
la solution 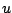 du problème dans le cas où la condition
initiale est une marche,
c'est-à-dire lorsque
du problème dans le cas où la condition
initiale est une marche,
c'est-à-dire lorsque
EPFL-IACS-ASN
