
Next: Le schéma décentré (ou Up: Equation de transport : Previous: Solution du problème de
Nous introduisons un pas spatial ![]() et un pas temporel
et un pas temporel ![]() . Nous définissons
ensuite
. Nous définissons
ensuite
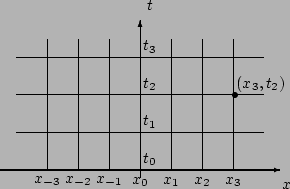
Soit ![]() la solution du problème (13.1) et (13.2).
Dans la suite,
les nombres
la solution du problème (13.1) et (13.2).
Dans la suite,
les nombres ![]() sont des approximations de
sont des approximations de
EPFL-IACS-ASN