
Next: Diffusion des schémas Up: Equation de transport : Previous: Le coefficient d'amplification (suite)
On dira que les schémas numériques sont stables (![]() -stables) lorsque le module
du coefficient
-stables) lorsque le module
du coefficient
![]() (ou le module des valeurs propres de
(ou le module des valeurs propres de
![]() lorsque
lorsque
![]() est une matrice) est inférieur ou égal à 1 indépendamment de
est une matrice) est inférieur ou égal à 1 indépendamment de ![]() , i.e.
, i.e.
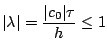 , i.e.
lorsque
, i.e.
lorsque
EPFL-IACS-ASN