
Next: Coefficient d'amplification Up: Equation des ondes : Previous: Un schéma de différences
Schématiquement les valeurs
![]() sont obtenues à partir des valeurs
sont obtenues à partir des valeurs
![]() et
et
![]() selon le diagramme suivant :
selon le diagramme suivant :
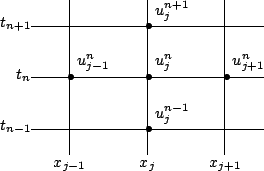
On obtient ainsi
Sous forme matricielle, (13.17)-(13.19) peut s'écrire
où
![]() est le vecteur de composantes
est le vecteur de composantes
![]() ,
, ![]() et
et
![]() sont les
sont les ![]() -vecteurs de composantes
-vecteurs de composantes
![]() et
et
![]() respectivement,
respectivement,
![]() est le
est le![]() -vecteur de
composantes
-vecteur de
composantes
![]() et
et ![]() est la
est la
![]() matrice
donnée par
matrice
donnée par
EPFL-IACS-ASN