
Next: Un schéma de différences Up: Equation des ondes : Previous: Solution de l'équation des
Nous introduisons un pas spatial
![]() , où
, où ![]() est un entier
positif, et un pas temporel
est un entier
positif, et un pas temporel ![]() . Nous définissons ensuite
. Nous définissons ensuite
Les noeuds ![]() et les temps
et les temps ![]() sont représentés dans la grille
ci-dessous :
sont représentés dans la grille
ci-dessous :
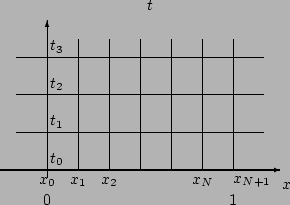
Soit ![]() la solution du problème (13.14)-(13.16). On note
la solution du problème (13.14)-(13.16). On note
![]() une approximation de
une approximation de
![]() ,
,
![]() et
et
![]() . Le schéma introduit dans le livre est un schéma de
différences finies explicite à deux pas de temps que l'on peut formuler de
la manière suivante :
. Le schéma introduit dans le livre est un schéma de
différences finies explicite à deux pas de temps que l'on peut formuler de
la manière suivante :
où la quantité ![]() est un facteur de correction (voir livre) donné par
est un facteur de correction (voir livre) donné par
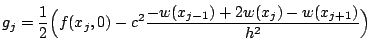
EPFL-IACS-ASN