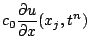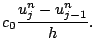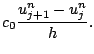Next: Etude de la stabilité Up: Chap. 14 : Approximation Previous: Cas particulier : équation
Si ![]() est un entier positif,
nous introduisons le pas spatial
est un entier positif,
nous introduisons le pas spatial
![]() et
les noeuds
et
les noeuds ![]() avec
avec
![]() .
Nous choisissons encore un pas
temporel
.
Nous choisissons encore un pas
temporel ![]() et calculons les temps
et calculons les temps ![]() ,
,
![]() .
Les points
.
Les points ![]() et
et ![]() sont représentés dans la grille ci-dessous :
sont représentés dans la grille ci-dessous :
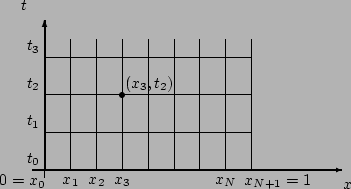
Si
![]() est la valeur de la solution du problème
(14.1)-(14.3) au noeud
est la valeur de la solution du problème
(14.1)-(14.3) au noeud ![]() et au temps
et au temps ![]() , nous notons
, nous notons
![]() son approximation (
son approximation (
![]() )
par le schéma
d'Euler progressif décentré.
)
par le schéma
d'Euler progressif décentré.
La condition initiale (14.2) se traduit par :