
Next: Formule composite de Gauss-Legendre Up: Chap. 3 : Intégration Previous: Formule composite du trapèze
On choisit ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
La formule composite devient
.
La formule composite devient
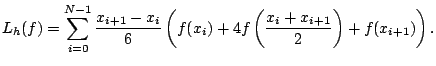 |
D'après le livre, si ![]() est quatre fois continûment dérivable, on a :
est quatre fois continûment dérivable, on a :
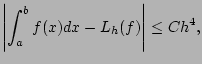 |
EPFL-IACS-ASN