Formule composite de Gauss-Legendre

Dans le cas de la formule de Gauss-Legendre à points, les points d'intégration sont les zéros du polynôme de Gauss-Legendre définis par

$\displaystyle L_{M}(t) = \dfrac{1}{2^{M} M !} \dfrac{d^{M}}{dt^{M}} (t^{2} - 1)^{M}.$

Les poids $\omega_1,\omega_2,...,\omega_M$ sont définis par

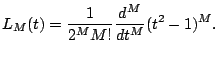
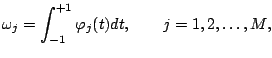$\displaystyle \omega_{j} = \int_{-1}^{+1} \varphi_{j}(t) dt, \qquad j = 1,2, \ldots, M,$

où $\varphi_{1}, \varphi_{2}, \cdots, \varphi_{M}$ est la base de Lagrange des polynômes de degré

associée aux

points

La simulation ci-dessous permet de visualiser $\int_a^b f(x)dx$ (aire entre la courbe rouge et l'axe des x) ainsi que (aire entre la courbe bleue et l'axe des x).

D'après le livre, si est fois continûment dérivable, on a :

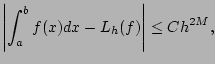$\displaystyle \left\vert \int_{a}^{b} f(x) dx - L_{h}(f) \right\vert \leq C h^{2M},$

où

ne dépend pas de

(ou

Par exemple, on choisit , $t_1=-1/\sqrt{3}$ , $t_2=+1/\sqrt{3}$ , $\omega_1=1$ , $\omega_2=1$ . La formule composite de Gauss-Legendre à deux points s'écrit

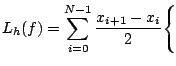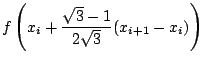$\displaystyle L_{h}(f) = \sum_{i=0}^{N-1} \frac{x_{i+1} - x_{i}}{2} \Biggl\{$	$\displaystyle f \left( x_{i} + \frac{\sqrt{3}-1}{2 \sqrt{3}} (x_{i+1} - x_{i}) \right)$
$\displaystyle +$	$\displaystyle f \left( x_{i} + \frac{\sqrt{3}+1}{2 \sqrt{3}} (x_{i+1} - x_{i}) \right)\Biggr\}.$

EPFL-IACS-ASN