Considérons le cas où 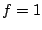 ,
,
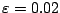 ,
, 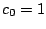 dans l'équation
(14.1).
Lorsque le temps
dans l'équation
(14.1).
Lorsque le temps 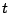 tend vers l'infini,
la solution
tend vers l'infini,
la solution 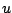 du problème (14.1)(14.2)(14.3)
tend vers la solution du problème
du problème (14.1)(14.2)(14.3)
tend vers la solution du problème
Ce problème est appelé "problème de couche limite" et est traité
dans la section 14.1 du livre.
L'exemple interactif suivant illustre le résultat du calcul
avec le schéma progressif décentré.
EPFL-IACS-ASN

![$\displaystyle -\varepsilon\dfrac{d^2 v}{d x^2}(x) +c_0 \dfrac{d v}{d x}(x)=1 \qquad x\in]0,1[,$](img823.png)