
Next: Une simulation interactive libre Up: Sur la convergence de Previous: Un exemple pour lequel
Soit ![]() définie par
définie par
![]() sur l'intervalle
sur l'intervalle ![]() .
Bien que
.
Bien que ![]() soit indéfiniment continûment
dérivable sur l'intervalle
soit indéfiniment continûment
dérivable sur l'intervalle ![]() ,
les grandeurs
,
les grandeurs
Dans l'exemple interactif suivant, la fonction ![]() (en rouge)
ainsi que le polynôme
(en rouge)
ainsi que le polynôme ![]() (en bleu) sont représentés.
Vous pouvez changer le nombre de points d'interpolations et constater
que l'interpolation de Lagrange avec une distribution uniforme
des points d'interpolation diverge. En revanche, si
les points d'interpolation sont choisis comme étant
les zéros des polynômes de Tchebycheff
(en bleu) sont représentés.
Vous pouvez changer le nombre de points d'interpolations et constater
que l'interpolation de Lagrange avec une distribution uniforme
des points d'interpolation diverge. En revanche, si
les points d'interpolation sont choisis comme étant
les zéros des polynômes de Tchebycheff
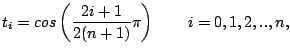 |
EPFL-IACS-ASN