
Next: Approximation de Galerkin Up: Chap. 11 : Une Previous: Problème de Poisson 2D
On considère le domaine
![]() comme étant le disque unité auquel on
a retranché un secteur circulaire d'angle
comme étant le disque unité auquel on
a retranché un secteur circulaire d'angle ![]()
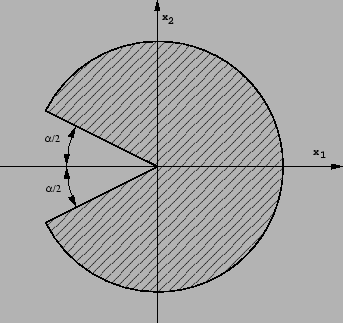
On choisit
![]() . Dans la figure ci-dessous,
nous avons représenté, pour diverses valeurs de
. Dans la figure ci-dessous,
nous avons représenté, pour diverses valeurs de ![]() , la dérivée
, la dérivée
![]() de la solution
de la solution ![]() du problème (11.1)
(11.2) par rapport à
du problème (11.1)
(11.2) par rapport à ![]() sur le segment horizontal
sur le segment horizontal
![]() .
.
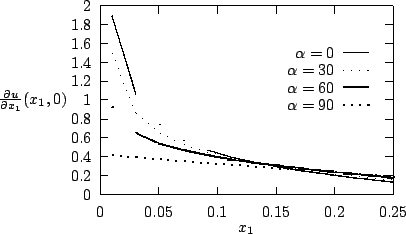
Nous remarquons que plus ![]() est petit, plus la solution devient ``peu régulière'' en
est petit, plus la solution devient ``peu régulière'' en
![]() . Le phénomène est compréhensible si nous interprétons
. Le phénomène est compréhensible si nous interprétons ![]() comme le
déplacement vertical d'une membrane chargée uniformément et attachée sur le bord
comme le
déplacement vertical d'une membrane chargée uniformément et attachée sur le bord
![]() de
de ![]() . En terme pratique, cela signifie que plus
. En terme pratique, cela signifie que plus ![]() est petit,
plus le point
est petit,
plus le point ![]() est une partie fragile de la membrane, depuis laquelle une déchirure
est susceptible de se former.
est une partie fragile de la membrane, depuis laquelle une déchirure
est susceptible de se former.
EPFL-IACS-ASN