Si 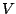 est l'ensemble de toutes les fonctions
est l'ensemble de toutes les fonctions
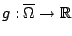 qui sont continues sur
qui sont continues sur
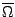 ,
nulles sur
,
nulles sur
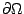 , et dont les premières dérivées partielles
, et dont les premières dérivées partielles
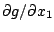 ,
,
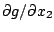 sont continues par
morceaux, la formulation faible (ou variationnelle) du problème
(11.1),(11.2) est de chercher
sont continues par
morceaux, la formulation faible (ou variationnelle) du problème
(11.1),(11.2) est de chercher 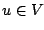 qui satisfait les
relations suivantes :
qui satisfait les
relations suivantes :
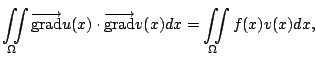 |
(11.3) |
pour toute fonction 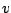 appartenant à
appartenant à 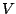 .
.
Un avantage important de la formulation (11.3) par rapport à la
formulation (11.1),(11.2) du problème de Poisson est que nous
faisons apparaître seulement des dérivées partielles premières dans
(11.3) alors que l'on a des dérivées secondes dans (11.1).
Une méthode de Galerkin pour résoudre numériquement (11.3) consiste à
1) fixer 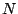 fonctions linéairement indépendantes
fonctions linéairement indépendantes
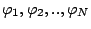 dans
dans 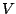 et décrire le sous-espace vectoriel
et décrire le sous-espace vectoriel 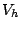 de
de 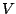 comme étant l'ensemble
des combinaisons linéaires des fonctions
comme étant l'ensemble
des combinaisons linéaires des fonctions
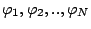 .
.
2) chercher une fonction
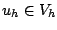 , c'est-à-dire chercher une combinaison linéaire
, c'est-à-dire chercher une combinaison linéaire
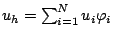 où les
où les 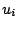 sont des nombres réels inconnus,
qui satisfait pour tout
sont des nombres réels inconnus,
qui satisfait pour tout
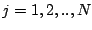 :
:
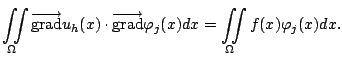 |
(11.4) |
EPFL-IACS-ASN

![]() est l'ensemble de toutes les fonctions
est l'ensemble de toutes les fonctions
![]() qui sont continues sur
qui sont continues sur
![]() ,
nulles sur
,
nulles sur
![]() , et dont les premières dérivées partielles
, et dont les premières dérivées partielles
![]() ,
,
![]() sont continues par
morceaux, la formulation faible (ou variationnelle) du problème
(11.1),(11.2) est de chercher
sont continues par
morceaux, la formulation faible (ou variationnelle) du problème
(11.1),(11.2) est de chercher ![]() qui satisfait les
relations suivantes :
qui satisfait les
relations suivantes :