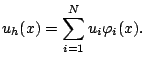En définissant les nombres
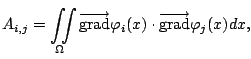 |
(11.5) |
nous constatons que la relation (11.4) est équivalente à
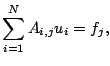
pour tout
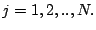
Si 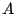 est la
est la
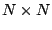 matrice de coefficients
matrice de coefficients
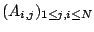 , si
, si 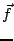 est le N-vecteur de
composantes
est le N-vecteur de
composantes
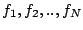 , alors la méthode de Galerkin est équivalente
à chercher un N-vecteur
, alors la méthode de Galerkin est équivalente
à chercher un N-vecteur 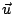 tel que
tel que
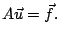 |
(11.6) |
Ayant 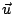 de composantes
de composantes
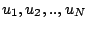 , on obtiendra
, on obtiendra 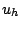 en
posant
On dira que
en
posant
On dira que 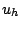 est une approximation de la solution
est une approximation de la solution 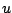 du problème
(11.3).
du problème
(11.3).
EPFL-IACS-ASN

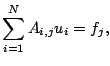 pour tout
pour tout