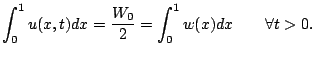Nous remarquons que
Il se trouve que
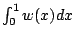 représente l'énergie du barreau au temps
représente l'énergie du barreau au temps 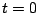 et que
et que
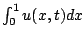 représente l'énergie du barreau au temps
représente l'énergie du barreau au temps 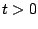 .
Nous avons donc montré que l'énergie reste constante au cours du temps,
ce qui est normal puisque le barreau est thermiquement isolé
et qu'il n'y a pas de source de chaleur.
.
Nous avons donc montré que l'énergie reste constante au cours du temps,
ce qui est normal puisque le barreau est thermiquement isolé
et qu'il n'y a pas de source de chaleur.
EPFL-IACS-ASN