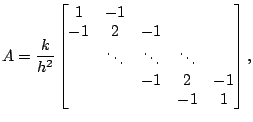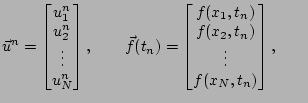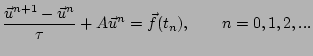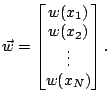Pour traduire le fait que
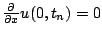 , nous posons
, nous posons
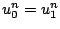 , pour tout
, pour tout
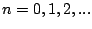 (en effet
(en effet
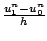 est une approximation par une formule de différences finies de
est une approximation par une formule de différences finies de
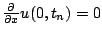 ). De même on pose
). De même on pose
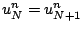 .
En tenant compte de ces relations,
nous pouvons écrire (12.16) sous la forme
.
En tenant compte de ces relations,
nous pouvons écrire (12.16) sous la forme
En définissant la
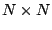 matrice
matrice 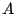 par
par
et les 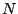 -vecteurs
-vecteurs 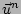 et
et
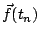 par
par
nous obtenons de façon condensée
Naturellement nous ajoutons une condition initiale
où 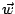 est le
est le 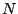 -vecteur défini par
-vecteur défini par
EPFL-IACS-ASN