Pour traduire le fait que
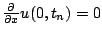 , nous ajoutons
artificiellement un noeud intérieur
, nous ajoutons
artificiellement un noeud intérieur 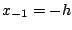 auquel
correspondrait une valeur d'approximation
auquel
correspondrait une valeur d'approximation 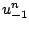 au temps
au temps 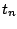 , et nous posons
, et nous posons
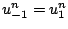 pour tout
pour tout
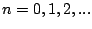 (en effet
(en effet
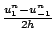 est une approximation par une formule de différences finies centrées de
est une approximation par une formule de différences finies centrées de
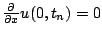 ). On procède de la même façon
en
). On procède de la même façon
en 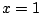 en introduisant un noeud
en introduisant un noeud 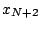 et on pose
et on pose
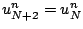 .
Nous avons donc introduit deux nouvelles inconnues
.
Nous avons donc introduit deux nouvelles inconnues 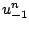 et
et 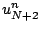 et il convient
donc d'ajouter deux nouvelles équations. Nous écrivons alors (12.16)
en prenant aussi
et il convient
donc d'ajouter deux nouvelles équations. Nous écrivons alors (12.16)
en prenant aussi 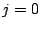 et
et 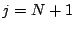 . Ainsi (12.16) avec
. Ainsi (12.16) avec
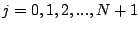 combiné
aux relations
combiné
aux relations
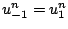 et
et
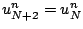 donne
donne
Ici encore le schéma peut se mettre sous forme vectorielle; nous obtiendrons
des vecteurs à 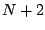 composantes.
composantes.
EPFL-IACS-ASN
