Pour obtenir le schéma d'Euler rétrograde, il suffit de modifier
(12.20)-(12.22) de la façon suivante :
avec bien entendu la condition initiale
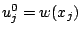 ,
,
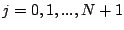 .
Le schéma (12.25)-(12.27) est un schéma implicite.
On ne peut pas obtenir directement les
.
Le schéma (12.25)-(12.27) est un schéma implicite.
On ne peut pas obtenir directement les 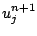 en fonction des
en fonction des 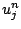 comme nous l'avons fait pour le schéma d'Euler progressif. Il faut résoudre
un système linéaire des
comme nous l'avons fait pour le schéma d'Euler progressif. Il faut résoudre
un système linéaire des 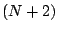 équations
(12.25)-(12.27) à
équations
(12.25)-(12.27) à 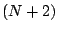 inconnues qui sont les
inconnues qui sont les
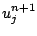 ,
,
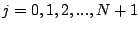 .
.
Subsections
EPFL-IACS-ASN
