D'après (13.6) et (13.7), nous savons que :
avec
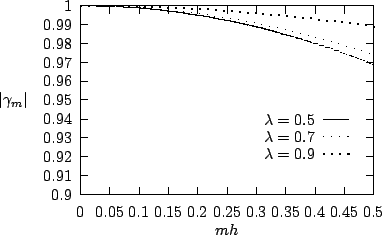
Nous avons représenté dans la figure suivante l'allure
de
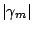 (et donc de la diffusion de la
(et donc de la diffusion de la 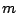 -ième harmonique)
en fonction de
-ième harmonique)
en fonction de 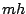 . Notons qu'il faut donc choisir
un nombre suffisant de points dans une période (
. Notons qu'il faut donc choisir
un nombre suffisant de points dans une période (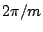 )
pour que la simulation soit réaliste. Nous avons donc représenté en
abscisse des valeurs de
)
pour que la simulation soit réaliste. Nous avons donc représenté en
abscisse des valeurs de 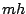 inférieures à
inférieures à 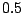 .
.
L'exemple interactif suivant illustre la diffusion numérique du schéma décentré.
EPFL-IACS-ASN