D'après (13.7), la dispersion est mesurée par :
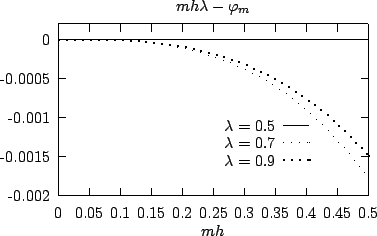
Dans la figure suivante, nous avons représenté l'allure
de
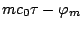 (et donc de la dispersion de la
(et donc de la dispersion de la 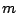 -ième harmonique)
en fonction de
-ième harmonique)
en fonction de 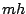 . Il faut remarquer que pour
. Il faut remarquer que pour
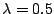 , il n'y a pas de
dispersion. C'est un cas particulier ! Vous pouvez en effet facilement
vérifier que, dans ce cas,
, il n'y a pas de
dispersion. C'est un cas particulier ! Vous pouvez en effet facilement
vérifier que, dans ce cas,
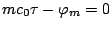 .
.
L'exemple interactif suivant illustre la dispersion numérique du schéma décentré.
EPFL-IACS-ASN