Nous avons déjà vu que, si
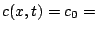 constante, si
constante, si
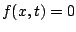 et si
et si
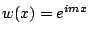 , alors
la solution du problème
(13.1) et (13.2) est donnée par :
Ainsi, nous obtenons :
, alors
la solution du problème
(13.1) et (13.2) est donnée par :
Ainsi, nous obtenons :
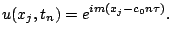 |
(13.13) |
D'autre part, d'après (13.6), nous savons que :
Posons
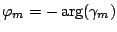 , c'est-à-dire
, c'est-à-dire
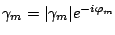 ,
nous avons donc
La quantité
,
nous avons donc
La quantité
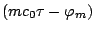 correspond au déphasage
introduit à chaque pas de temps
entre la solution exacte et la solution numérique lorsqu'on
propage la
correspond au déphasage
introduit à chaque pas de temps
entre la solution exacte et la solution numérique lorsqu'on
propage la 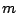 -ième harmonique. On dit alors qu'il y a
dispersion de la
-ième harmonique. On dit alors qu'il y a
dispersion de la 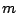 -ième harmonique. Plus
-ième harmonique. Plus
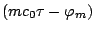 est grand et plus la dispersion de la
est grand et plus la dispersion de la
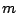 -ième harmonique est grande.
-ième harmonique est grande.
Subsections
EPFL-IACS-ASN
