
Next: Comparaison de la dispersion Up: Dispersion des schémas Previous: Schéma de Lax-Wendroff
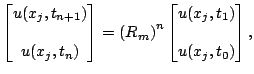
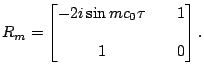
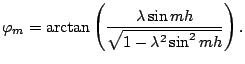
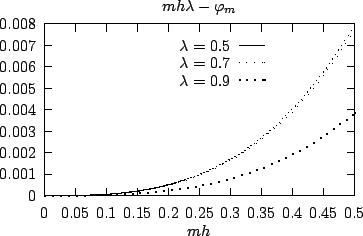
Nous avons représenté dans la figure suivante l'allure
de
![]() (et donc de la dispersion de la
(et donc de la dispersion de la ![]() -ième harmonique)
en fonction de
-ième harmonique)
en fonction de ![]() .
.
L'exemple interactif suivant illustre la dispersion numérique du schéma saute-mouton.
EPFL-IACS-ASN