Nous allons maintenant chercher les positions
des billes 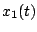 et
et 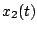 sous la forme
sous la forme
les grandeurs 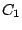 ,
, 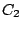 et
et 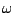 étant inconnues.
Injectons ces relations dans les
équations du mouvement.
Puisque
étant inconnues.
Injectons ces relations dans les
équations du mouvement.
Puisque
nous obtenons, après avoir simplifié par
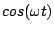
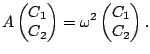 |
(7.1) |
Le problème revient donc à chercher 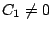 ,
,
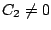 et
et 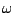 tels que
les deux équations ci-dessus soient satisfaites.
tels que
les deux équations ci-dessus soient satisfaites.
EPFL-IACS-ASN
