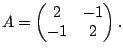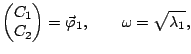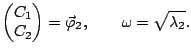Soit 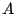 la matrice définie par
la matrice définie par
Supposons connaître les deux
valeurs propres et vecteurs propres de la matrice 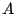 , i.e.
, i.e.
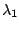 ,
,
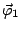 ,
, 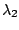 ,
,
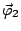 tels que
tels que
Puisque 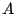 est symétrique définie positive, les valeurs propres
est symétrique définie positive, les valeurs propres
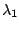 et
et
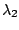 sont réelles strictement positives.
Les grandeurs
sont réelles strictement positives.
Les grandeurs 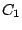 ,
, 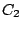 et
et 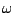 solutions de (7.1) sont
alors données par
solutions de (7.1) sont
alors données par
ou encore
EPFL-IACS-ASN

![]() la matrice définie par
la matrice définie par